 The Model
The Model

As was mentioned earlier Einstein's assumptions, that the liquid is composed of atoms which are in constant motion, provide the correct qualitative results for describing Brownian motion. However the question still remains, Does Einstein's model predict the correct quantitative results?
Now we wish to discuss the concept of displacement and how it pertains to a suspended body undergoing Brownian motion. First of all there is a major difference between distance traveled and your displacement. The figure below demonstrates the major difference between the meanings of these two words.
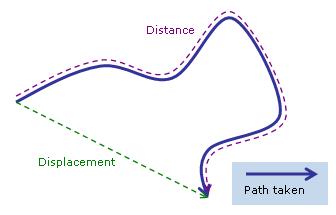
As you can see when we refer to distance, we are referring to the length of the entire path that you traveled. In the above figure the distance is represented by blue line. However, when we refer to displacement, we are referring to the difference between where you started and where you ended.
CLASSICALLY
For a classical particle, like a billiard ball or a car, the displacement is proportional to time. This means that if I was driving to the grocery store I wanted to figure out my displacement from home, I would take my velocity and multiply it by the time it took for me to get there! This may be expressed mathematically as
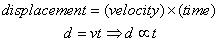
We can see that the displacement is proportional to time for classical bodies.
BROWNIAN MOTION
For a suspended body undergoing Brownian motion, experiments have shown that it's displacement is proportional to the square root of time. This may be expressed mathematically as
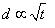
As a result, there is a large discrepancy between what we would expect of a classical particle and a particle undergoing Brownian motion! The figure below shows this difference graphically.
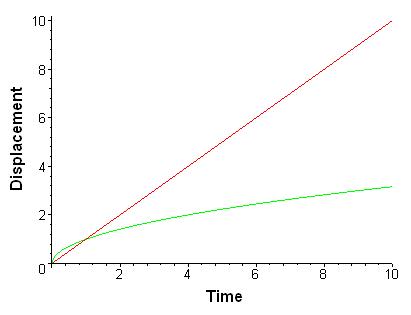
From this figure, even after 10 units of time there is a large discrepancy between the classical displacement in red and the Brownian motion displacement in green.
Using a statistical analysis Einstein determined the displacement of a suspended body in a liquid to be
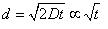
In this equation, D, is known as the diffusion coefficient. It is also observed that Einstein's derived expression quantitatively matches the displacement found from a Brownian motion experiment.
It should be noted that each atom in the liquid can be treated like a semi-classical particle meaning its displacement is directly proportional to time. However, once statistics are taken into account for the entire ensemble of particles the derived result of the displacement is proportional to the square root of time.
For an excellent summary of Einstein's motivation through his derivation please visit Ann. Phys. 14, Supplement 23-27 (2005). 11
You may also view my own article where I summarize the first two sections of Einstein's paper.