Ampere's Law:

A changing magnetic field produces an electric field. This is expressed explicitly in one of a set of equations called Maxwell's Equations. This particular Maxwell Equation is called Ampere's Law. If you don't understand what this equation means, don't panic.

 

 

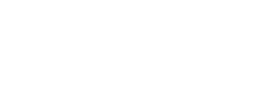
If you remember grade 9 math, the equation for the slope of a line was :

 

 

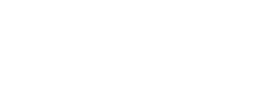
The curly symbol ∂ is similar to the delta symbol Δ in that they both represent a change in a quantity. The only difference is that the curly symbol∂implies that the difference in said quantity is infinitely small. For example, ∂y = (y_2 - y_1) when y_1 is infinitely close to y_2.

Now let's look at Ampere's Law again. The E, B and the t represent eletric field, magnetic field and time respectively. From what was discussed earlier, the right hand side of that equation means infinitely small change in magnetic field over infinitely small change in time. This is the instantaneous rate of change. Because of the equality, the change in magnetic field over time generates an electric field. The ∇ X symbol is a differential operator called the curl. When acted on E, it represents the rotation due to E at a given point, hence the name 'curl'.

Radiation Emission:

Consider a point charge with non-uniform acceleration. As the charge is accelerated, its electric field is oriented perpendicular to the velocity of the charge.

[1]

If you set the path such that there is non uniform acceleration and high velocity, you will notice this; The red arrow is will be perpendicular to the white line. These are points where the electric field "curls". Because of Ampere's Law, the curl of the electric field produces a changing magnetic field.

The magnetic field also has a curl. This produces a changing electric field as expressed in a Maxwell Equation called Farraday's Law.

 

 

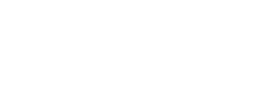
(Farraday's Law in free space)

This looks very similar to Ampere's Law except that the B and E have been switched around.

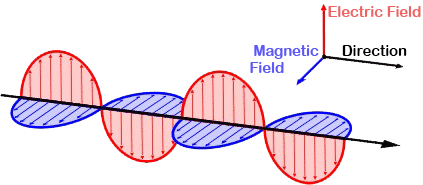
This changing electric field producing a magnetic field which in turn produces an electric field and so on, defines the electromagnetic wave.

 

 

 

[2]

 

 

The result is an oscillating electric field with an oscillating magnetic field perpendicular to it, all propagating at the speed of light. The faster they oscillate, the higher the frequency of the EM wave.

Next