Angular momentum:

Angular momentum is the momentum of a rotating mass, or a rotating system of masses. Similar to linear momentum, angular momentum is also conserved under the law of conservation of angular momentum.

 

 

The moment of inertia is a specific quantity for a single mass or a system of different masses, which describes the spatial distribution of mass. Consider a system of masses that are so small, they can be considered to be a single point, as displayed in the diagram below.

 

 

 

 

 

 

 

 

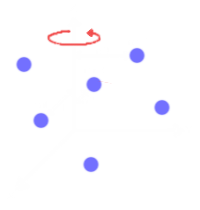
The moment of inertia of this system can be described as the sum of the squared distance of each mass to the axis about which the system is rotating, multiplied by their respective mass, as shown below.

 

 

This quantity gives a spatial distribution of mass that helps describe how angular momentum is related to angular velocity, given in rotations per second. Consider the masses being a large distance away from the axis of rotation. At a given angular velocity, the angular momentum of the system would be much larger than if the masses were all close to the axis of rotation. However, if one were to set the system in motion, and bring the masses closer to the axis, since angular momentum is the quantity that is conserved, the moment of Inertia reduces, and angular velocity increases. This can be visualized by picturing a spinning figure skater with her arms out quickly pulling her arms in, thus reducing her rotation speed.

The moment of inertia for a large solid body is calculated using a similar method, but more complicated techniques.

Next