 Statistical Model
Statistical Model

The important fact to remember about how Brownian motion is applied to the modern day world, is that it is the statistical model for describing Brownian motion which is used in applications NOT the phenomenon of Brownian motion itself. The statistical model is referred to as the Brownian motion function, and it is this function that has a wide range of applications.
1. Independent: This means that where you are right now does not effect where you are going to be. An example of a motion that is dependent is a ball on the hill. If the ball is at the top of the hill it must roll down. We conclude that it's next position is directly related to it's postion the moment before.
2. Isotropic: This means that you are just as likely to move in any direction. There is NO preferred direction of travel.
3. Random: This means that you do not know how much you are going to move in that direction.
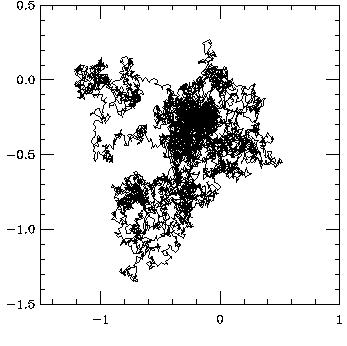
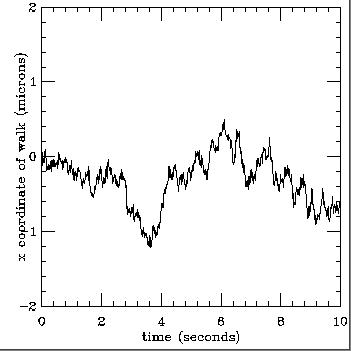
This Brownian motion function can be graphed in 1 dimension or 2 dimension, depending on the form required to describe your phenomenon. Examples of both the 1 dimensional and the 2 dimensional Brownian motion functions are shown below.
2D BROWNIAN MOTION FUNCTION